
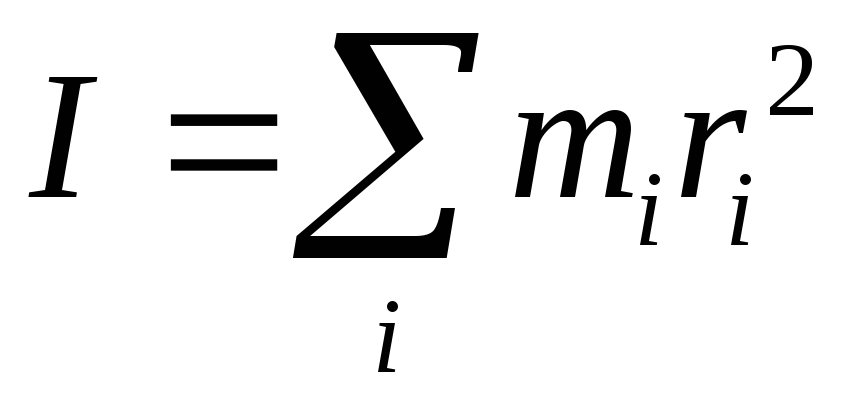
Step 2: For the integral limits, we have to count with respect to the axis of rotation. What matters is that we use the same letter so that we can integrate with respect to it.
Note that in the integral our variable is r, so we can set dL = dr, because it doesn’t matter how we call our distance. Because the linear density is constant, what we get is simply: dm = λ*dL. We therefore have the following expression for the mass: m = λ*L.īut we want to have the expression for an infinitesimal mass dm.
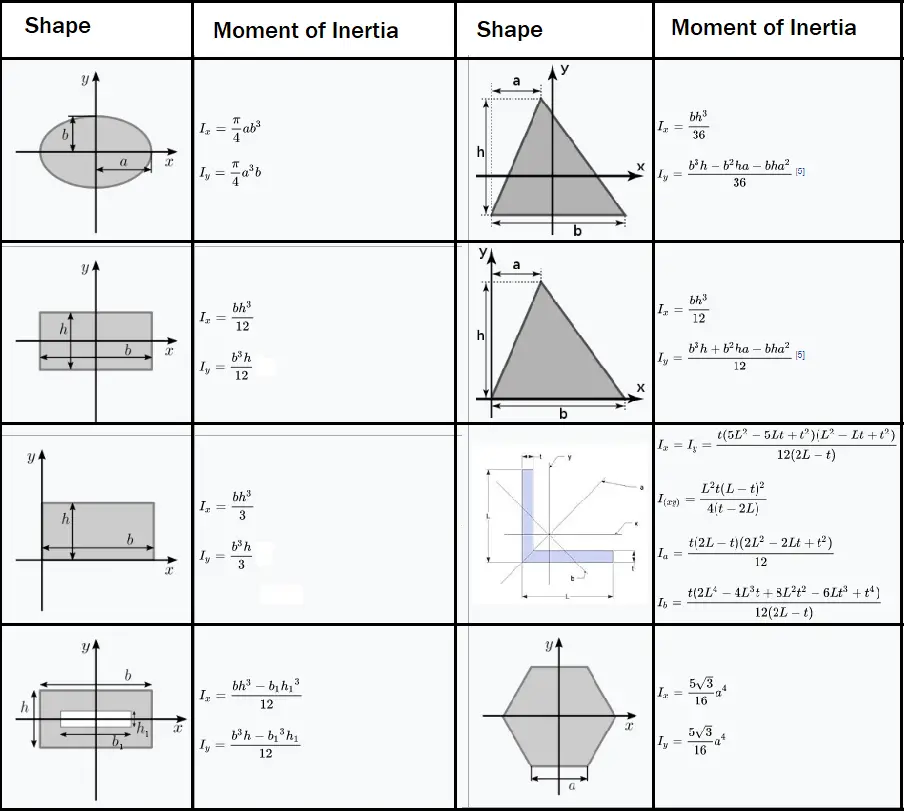
And instead of density ρ, which is defined for three-dimensional objects, we use λ, which is linear density. Now, because in our example we have a rod, we have a one-dimensional object, so instead of Volume we use Length. Step 1: The density is defined as ρ = m/V, so in terms of mass we have: m = ρ*V. Examples Example 1Ī rod of length L and mass m is rotated about its centre as seen in the picture. Step 4: Substitute the density to get the answer in terms of the mass of the body. Step 2: Find the integral limits with respect to the axis of rotation. Step 1: Express dm as a function of r with the help of the density. The moment of inertia depends on the mass distribution and on the axis of rotation. This is analogous to how the mass determines the force needed for a certain linear acceleration. Moment of Inertia formulaĭefinition: The moment of inertia is a quantity that determines the torque that is needed to achieve a certain angular acceleration about a given axis. In other words, the mass, the shape and the axis of rotation influence the moment of inertia of a rotating body. This means that for the moment of inertia, both the mass and the distance to the mass (or how the mass is distributed with respect to the axis of rotation) is important. So, if we take the same football and tie it to a rope that is double the length, then the football will be double the distance from us, and it will be much harder to rotate. What do we mean by distribution of the mass? By that we mean how far the mass is from the axis of rotation. So, shouldn’t the moment of inertia simply be the mass of the object, since it behaves the same way? The answer is no, because there is another property that influences the moment of inertia: the distribution of the mass. However, if we tie a football with a rope, we can see that it is much more difficult to rotate, since it has more mass. If we imagine a marble tied to a string, we can rotate it easily. In the same sense, an object with a larger moment of inertia (rotational mass) is more difficult to rotate. To better understand the analogy: If an object has a large mass, like a car, it is more difficult to move than an object with a lesser mass. Once again, we see the analogy of mass m and moment of inertia I. If the body is rotating, then there is additional energy going into making the rotation possible, and we account by the rotational kinetic energy: KE=1/2*I*ω 2. The total energy of a system (kinetic + potential) is normally conserved, so KE is useful in many exercises. The linear kinetic energy is defined by KE=1/2*m*v 2. Again, we see here that the moment of inertia I is the rotational analogy of the mass m. Therefore, the momentum is a useful formula that can be used to calculate the mass or velocity of the objects that make up a system.īut in the case that the objects are rotating, we need another formula, which is the angular momentum: L=I*ω, where ω is the angular velocity. The momentum of a system remains constant if there are no forces applied.

Therefore, I is a kind of “rotational mass”, which we call moment of inertia. The most famous one is Newton’s second law: F = m*a.īut what if we have a rotating body? In that case we have an analogous formula, which is Newton’s second law for rotation: τ = I*α, where τ is the torque (analogous to the force) and α is the angular acceleration (analogous to the linear acceleration). The mass of an object is an important quantity for several equations. In essence, the moment of inertia is the rotational analogy for the mass of an object. The moment of inertia might be a difficult concept for students, but with the right analogies it can be understood easily.


 0 kommentar(er)
0 kommentar(er)
